Nuevas formas para determinar fractales en el ADN
Eduardo Sánchez Ortega y Laura Vargas-Parada
Julio 26, 2018
No. 26/2018
Ilustración: Joram Patiño, 2018
“El verdadero espíritu del deleite, de la exaltación,
del sentimiento de ser más que humano,
que es la piedra de toque de la más alta perfección,
ha de buscarse en las matemáticas al igual que en la poesía”
—Bertrand Russell
“Apenas hoy en la mañana, mi estudiante Omar Suárez y yo, tuvimos un resultado que nos tienen muy contentos”, dijo con visible entusiasmo Pedro Miramontes, profesor titular de tiempo completo y miembro del grupo de Biomatemáticas de la Facultad de Ciencias de la UNAM al arrancar su presentación Avances recientes en la geometría fractal del DNA dentro del Coloquio del Centro de Ciencias de la Complejidad el pasado 3 de mayo. Explicó que al seminario le puso “avances recientes” porque se trata de un tema que ha trabajado desde hace muchos años, pero no de manera continua. Sin embargo, los nuevos resultados anticipan “un proyecto bien sólido de investigación para los próximos años”.
El DNA –o ácido desoxirribonucleico— es el medio que utilizan los sistemas biológicos para guardar información. Es una molécula construida a partir de largas secuencias de cuatro moléculas más pequeñas llamadas nucleótidos, usualmente designados como A, C, T y G. Si en un medio electrónico la información se guarda en secuencias binarias de ceros y unos, los sistemas biológicos almacenan información en secuencias de nucleótidos: A, C, T y G. En esas secuencias se almacenan todas las instrucciones para que un organismo pueda funcionar.
Describir la estructura del DNA fue polémica: una carrera muy competida entre grupos de investigadores que sabían que quien lograra esclarecer el asunto tendría asegurado un Premio Nobel. La finalmente descubierta estructura de la doble hélice esconde motivos estructurales muy bellos pero que no son visibles de manera directa. Uno de ellos es un fractal que es un reflejo de la estructura de correlaciones de las cuatro letras en una secuencia genómica.
Sobre por qué construir y estudiar fractales en el DNA, Miramontes recordó un ensayo del matemático húngaro Eugene P. Wigner, “ La efectividad irracional de las matemáticas en las ciencias naturales”, donde el también físico teórico e ingeniero reflexiona cómo resultados matemáticos que aparentemente nada tienen que ver con las ciencias naturales al final resultan descripciones de fenómenos naturales. “La matemática nos asombra porque es parte de las ciencias naturales”, dijo Miramontes, y analizar desde una perspectiva matemática la estructura del DNA podría develar nuevos misterios de tan extraordinaria molécula.
CONSTRUYENDO FRACTALES A PARTIR DEL DNA
Partiendo de la estructura del DNA, el investigador identifica nucleótidos grandes (aquellos que están conformados por dos anillos, la G y la A), y dos moléculas pequeñas que sólo contienen un anillo en su estructura (la C y la T).
Además, dentro en la doble hélice de DNA, las G están unidas a las C por un triple enlace de hidrógeno. A las G y C se les denominará letras fuertes. Por su parte, las A están unidas a las T por un doble enlace de hidrógeno y, en consecuencia, a las A y T se les denominará letras débiles.
De esta forma, explica Miramontes, bastan las cuatro letras que componen el polímero de toda la molécula de DNA para generar dos dicotomías: la dicotomía fuerte (GC) y débil (AT), y la dicotomía grande (AG) y pequeña (CT); cada dicotomía con sus peculiaridades físico químicas y geométricas.
Aclara que en su investigación sólo se utiliza la información contenida en el DNA nuclear –el DNA contenido en el núcleo celular o genoma nuclear—. Explica que también hay DNA (genoma mitocondrial) dentro de las mitocondrias, una estructura celular que, entre otras funciones, se encarga de proveer de energía a las células.
Una regla más. Lo que se conoce como principio de complementaridad: en una doble hélice de DNA, siempre que hay una G en la otra hélice habrá una C, y siempre que hay una T, estará apareada con una A. De tal forma que si conozco la información de una de los lados de la doble hélice el otro estará determinado.
De esta forma, “para un matemático el genoma nuclear puede verse como una sucesión Xi de i hasta n sobre un alfabeto de 4 símbolos”, concluyó Miramontes.
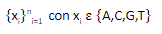
Luego, con un sistema parecido al “juego del caos” –método matemático que permite crear un fractal usando un polígono y un punto inicial dentro de éste seleccionado al azar— se agrupan de tres formas distintas las bases nitrogenadas de una secuencia de DNA formando un sistema binario que arroja puntos en un plano a partir de los cuales se forma el fractal.
“Los fractales son la única figura de la naturaleza en la cual cada parte es igual al todo”, dijo Miramontes. Esta propiedad se debe a una característica de un grupo grande de fractales llamada autosemejanza (self similarity).
Los fractales abundan en la naturaleza –como las hojas de las plantas, los corales, el brócoli Romanesco, la forma de las nubes— y se pueden generar mediante varios mecanismos. Uno es por autosemejanza, donde los patrones o formas se repiten, como el triángulo de Sierpinski; o bien, pueden ser métodos matemáticos como los atractores extraños de sistemas dinámicos, como el Atractor de Lorenz o el Conjunto de Mandelbrot, donde debido a la presencia de comportamientos extraños en los sistemas dinámicos se forman patrones; o puede darse por ramificación, como en los conductos aéreos de los pulmones donde un conducto se divide en dos, y esos dos nuevos conductos se dividen en otros dos, etcétera.
También se pueden modelar fractales con ayuda de las computadoras a partir de funciones iteradas, es decir, funciones compuestas por la misma función que se aplica una y otra vez sobre sí misma.
GEOMETRÍA FRACTAL DEL DNA
La idea de la fractalidad del DNA no es nueva. Se trabaja prácticamente desde que hubo secuencias de nucleótidos disponibles para su análisis.
Inicialmente se utilizaron herramientas de análisis de series de tiempo para evaluar las secuencias de DNA –esto es, el análisis de un fenómeno o variable X y su dinámica a lo largo del tiempo—.
Lo que es un poco más reciente es el juego del caos. En 1990, H. Joel Jeffreys, de la Northern Illinois University, utilizó el juego del caos con la secuencia de DNA del gen de la beta globina humana localizado en el cromosoma 11; una secuencia de unos 80 nucleótidos o letras. Etiquetando los vértices de un cuadrado con A, C, G y T, y siguiendo las reglas del juego, obtuvo estructuras con geometría fractal. En aquel entonces no se había secuenciado el genoma humano completo.
Para el trabajo de investigación que Miramontes realiza en colaboración con Diana Rivera del Instituto de Matemáticas campus Morelos y Omar Suárez de la Facultad de Ciencias de la UNAM, retoma las dicotomías del DNA y menciona que existe una tercera dicotomía de naturaleza fisicoquímica (T-G, A-C) llamada bases amínicas o cetónicas. Dadas dos dicotomías la tercera estará completamente determinada. Esto permite traducir de tres formas distintas un genoma a 0’s y 1’s.
“Un fragmento de DNA, no importa de qué naturaleza sea, puede traducirse a secuencias binarias y las secuencias binarias son muy convenientes para trabajar ya que hay muchas herramientas para su análisis matemático”, explicó el matemático.
De esta forma se tienen tres diccionarios. El primer diccionario es fuertes y débiles, las fuertes son unos y las débiles son ceros. El segundo son grandes (unos) y pequeños (ceros); y para el tercero las bases amínicas se consideran ceros y las cetónicas unos.
Una vez que se tienen las tres secuencias binarias, el investigador propone una función que relacione las dos primeras secuencias para determinar la tercera: la función XOR. La conversión de números binarios a números fraccionarios permite construir una sucesión de puntos en el espacio lo que resulta en una gráfica 3D con un patrón fractal de autosemejanza: un tetraedro de Sierpinski. Si el tetraedro es proyectado en 2D, se obtiene una figura con patrón fractal conocido como alfombra de Sierpinski.
Los trabajos de Miramontes y colaboradores, consiste en considerar el procedimiento anterior con diferentes tipos de DNA, obteniendo figuras con patrones fractales, algunos completamente distintos entre sí ( cromosoma 21 del humano y cromosoma de una bacteria) y otros muy similares ( cromosoma 21 del humano y cromosoma de la rata).
AVANCES RECIENTES
Lo reciente en su trabajo de investigación, explica Miramontes, es el uso de sistemas de iteraciones. Lo que Miramontes y colaboradores encontraron fue un perfil idéntico en el mapeo del cromosoma 21 del ser humano con el mapeo de un sistema dinámico determinista. “Esto nos sugiere la existencia de un sistema dinámico subyacente en la evolución de las genomas, al menos en el genoma del humano”, explicó.
Otro trabajo reciente utiliza matrices markovianas donde como parámetros de control se considera el contenido de CpG (C seguida de G) en cada genoma y el porcentaje de cuánto es una C seguida de una G. Encontraron que los organismos unicelulares que han analizado se encuentran por encima de un cierto parámetro o línea de CpG. Por su parte, por debajo de dicho parámetro se encuentran los organismo multicelulares que han analizado. Es decir, en términos físicos, existe una transición de fase para las variables de control CpG y %CpG.
Finalmente, Miramontes compartió el promisorio resultado de aquella mañana. Poco antes del coloquio, Omar construyó un fractal a partir del genoma de una bacteria y luego, por medio de la computadora, generó un genoma artificial con la misma matriz de dímeros. Lo que obtuvo fue inesperado: una figura fractal idéntica a la figura fractal obtenida para la bacteria.
“Si podemos interpretar adecuadamente esto, entonces la división de los dos grandes súper reinos en la evolución biológica (eucariontes y procariontes) no es continua sino abrupta”, sugirió Miramontes.