Encontrando la ruta más eficiente: una aproximación

Por Brenda Garduño Sánchez

27 de julio de 2018

Un repartidor de pan visita quince tiendas en su ruta de distribución. La ruta más eficiente es aquella que ocupa el menor tiempo y cantidad de combustible posible. ¿Cómo decidir cuál será el orden en el que se visitará las tiendas?

Por décadas se han diseñado algoritmos que sugieren los caminos más cortos para la resolución de este tipo de problemas. Pero, ¿qué pasa cuando los sitios se mueven en el tiempo? Por ejemplo, cuando una tienda deja de comprar el producto y otra, en un sitio completamente distinto se agrega a la ruta del repartidor. ¿Cómo optimizar la ruta cuando el destino cambia continuamente?

Para analizar el problema, un equipo internacional de investigadores utilizó un problema matemático computacional muy conocido llamado “problema del agente viajero” (Traveling Salesman Problem o TSP por sus siglas en inglés) —que intenta encontrar la ruta más corta posible en la que se pueda visitar un sitio una sola vez y regresar al punto de partida—. Lo nuevo de este trabajo es que los investigadores decidieron estudiarlo cuando los sitios a visitarse no son estáticos.

“Las rutas más cortas o más largas son más estables que las de longitudes intermedias al poner o quitar nuevos sitios”, concluyen investigadores del Centro de Ciencias de la Complejidad (C3), Instituto de Física e Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas de la UNAM, CDMX; el Massachusetts Institute of Technology, Estados Unidos; la ITMO University, Rusia; la Aalto University School of Science, Finlandia y la University of Viena, Austria.

Los resultados se publicaron el pasado 16 de abril en la revista científica Complexity.

https://www.hindawi.com/journals/complexity/2018/2826082/fig1/

---

---

Tradicionalmente, para resolver problemas de optimización se estudian sitios que no se mueven en el tiempo (un TSP estático). Sin embargo, se han propuesto modificaciones al TSP tradicional generando nuevas variantes.

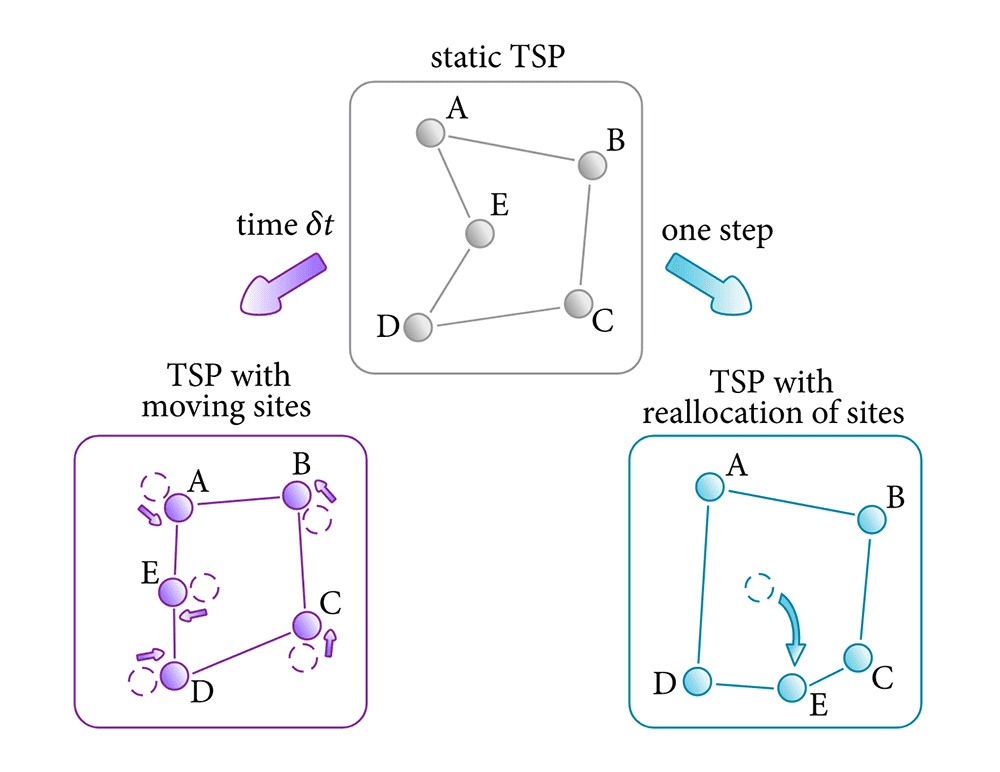
En este caso, los investigadores proponen estudiar condiciones no estáticas con sitios que se mueven y sitios reasignados. En ambos casos los sitios cambian su posición con respecto al tiempo. A este modelo los investigadores lo denominan TSP no estático o dependiente de tiempo.

El TSP con sitios móviles (bTSP) es un problema en el que los sitios se comportan como barcos, los cuales se mueven a una velocidad constante y en línea recta. Por su parte, en el TSP con sitios reasignados (rTSP) un solo sitio se mueve de manera aleatoria a una velocidad no constante.

“Ambos algoritmos son diferentes, pero al final de cuentas el problema donde hay reasignación de sitios es un escenario más general en cual entra un caso más particular donde los sitios se mueven en línea recta a una velocidad constante como barcos” explica Carlos Gershenson, uno de los autores del estudio. “El objetivo del trabajo fue ver qué tanto cambian las trayectorias cuando mueves tantito de lugar alguno o varios de los sitios”. Para ello, los investigadores evaluaron la dinámica de rango en todas las trayectorias generadas para el bTSP y el rTSP.

La asignación de rangos de las trayectorias se hizo de acuerdo a su longitud. Las trayectorias más cortas se asignaron con el rango más bajo y las más largas con el rango más alto.

Para evaluar el número de trayectorias que hay dentro de cada rango en un periodo de tiempo los investigadores analizaron el ranking de las trayectorias cada vez que se movían los sitios en el bTSP y el rTSP. Así se pudo evaluar y observar la diversidad de rangos, lo que los autores refieren como el número de trayectorias que hay dentro de cada rango en un periodo de tiempo.

De esta forma se pudo determinar la estabilidad de las trayectorias en el tiempo, es decir, si las trayectorias se mantenían en el mismo ranking a lo largo del tiempo, o no.

Finalmente observaron que a pesar de que ambos modelos, el rTSP y el bTSP, tienen diferentes aproximaciones, ambos se comportan de manera muy similar. En ambos las trayectorias de longitud más corta y más larga se mantienen estables, “son más robustas al cambio”, señalan los autores en el artículo científico. Esta novedosa aproximación sugiere que una vez que la solución óptima es alcanzada, ésta debería ser más estable que las no óptimas.

Bajo esta óptica, la ruta más óptima para el repartidor de pan no variará mucho si alguna de las tiendas a visitar cambia.

LIGAS:

Paper:https://www.hindawi.com/journals/complexity/2018/2826082/

Descargar el pdf