Usando la interdisciplina para estudiar los números primos

Por Felipe Jiménez Rodríguez

07 de septiembre de 2018

Los problemas que abordan las ciencias de la complejidad no pueden resolverse desde las disciplinas tradicionales de la investigación. Para estudiar la dinámica de la contaminación atmosférica, la dispersión de enfermedades producidas por mosquitos o la salud de los ecosistemas hay que echar mano de un abanico de herramientas provenientes de distintas disciplinas, es decir, la interdisciplina emerge ante la naturaleza de los problemas a resolver.

En un artículo publicado en la revista Entropy en febrero pasado, investigadores del Centro de Ciencias de la Complejidad (C3) y del Instituto de Física de la UNAM; la Universidad Politécnica de Madrid y la Queen Mary University of London abordaron una teoría matemática (la teoría de números) desde la perspectiva de la física (sistemas dinámicos). “Mostramos cómo la transferencia interdisciplinaria de técnicas desde la teoría de sistemas dinámicos a la teoría de números puede ser un camino fructífero para la investigación”, escriben los autores en el artículo.

Para su análisis, los investigadores utilizaron herramientas de la dinámica no lineal y simbólica, tales como el espectro de entropías de Rényi y el juego de caos para estudiar tres secuencias de símbolos asociadas a los números primos. En las secuencias estudiadas se encontró comportamiento aleatorio en una ellas y dos secuencias con comportamiento caótico. “Caos y aleatoriedad son cosas diferentes. Caos es una comportamiento que parece aleatorio, pero con un origen que en realidad sí es posible determinar”, explica Octavio Miramontes autor sénior del artículo vía correo electrónico.

Los investigadores esperan que este artículo sirva como inspiración a los matemáticos para ver problemas tradicionales usando una mirada diferente y al mismo tiempo inspirar a los científicos naturales a estudiar las estructuras matemáticas como si fueran observaciones experimentales con leyes subyacentes que permiten un análisis científico.

http://www.mdpi.com/1099-4300/20/2/131/htm

---

---

Un número primo es un número natural mayor que 1 que tiene únicamente dos números que los dividen de forma exacta: él mismo y 1, por ejemplo, 2,3,5,7, etc. Los números primos son infinitos y “... son esenciales para la vida diaria, por ejemplo en la criptografía que hace segura la internet. Los portales bancarios y las transacciones con tarjetas de crédito en internet solo existen gracias a los primos”, explica Miramontes.

Los números primos pueden dividirse en dos grandes conjuntos. Aquellos que al dividir entre 4 sin tomar en cuenta decimales, el residuo (o restante) es 3, como el 7 u 11; se les llama primos gaussianos. Por otro lado, los números primos cuyo residuo que resulta de dividir entre 4 es 1 se llaman pitagóricos, por ejemplo el 5 o 13. La secuencia principal de números primos se alterna entre estos dos grupos de primos sin un orden aparente.

Se estudiaron tres secuencias diferentes asociadas a la secuencia de los números primos.

La primera secuencia estudiada es la de transiciones (o saltos) entre los primos gaussianos y los pitagóricos. La segunda secuencia es la de los residuos que resultan de dividir los primos entre un número entero k sin tomar en cuenta decimales, donde k es un número entero. La tercera secuencia estudiada se construye de la siguiente manera: primero se observa cuántos números hay entre cada par de primos consecutivos, luego ese número entre primos se divide entre seis, sin tomar en cuenta los decimales, y se ve cuál es el residuo. Por ejemplo, entre los primos 89 y 97 hay 8 números de diferencia, el residuo resultante al dividir 8 entre 6 es 2 (8 = 6 x 1 + 2). La secuencia estudiada es la de estos residuos resultantes.

Los investigadores estudiaron las secuencias para determinar si se presentaba un comportamiento aleatorio (totalmente azaroso) o por el contrario un fenómeno caótico determinista, es decir, un fenómeno que su comportamiento parece aleatorio pero en realidad no lo es.

Para saber si una secuencia de símbolos es totalmente azarosa se compara con una segunda secuencia construida con los mismos elementos de la primera pero colocados de forma aleatoria, a este tipo de secuencias aleatorias se les llama modelos nulos.

A las secuencias de símbolos también se les aplicó un conjunto de medidas llamadas el espectro de entropías de Rényi. Las entropías cuantifican la diversidad, incertidumbre o aleatoriedad de un sistema. Si los valores de entropía de los modelos nulos coinciden con los valores de las secuencias reales hay indicios de un comportamiento aleatorio.

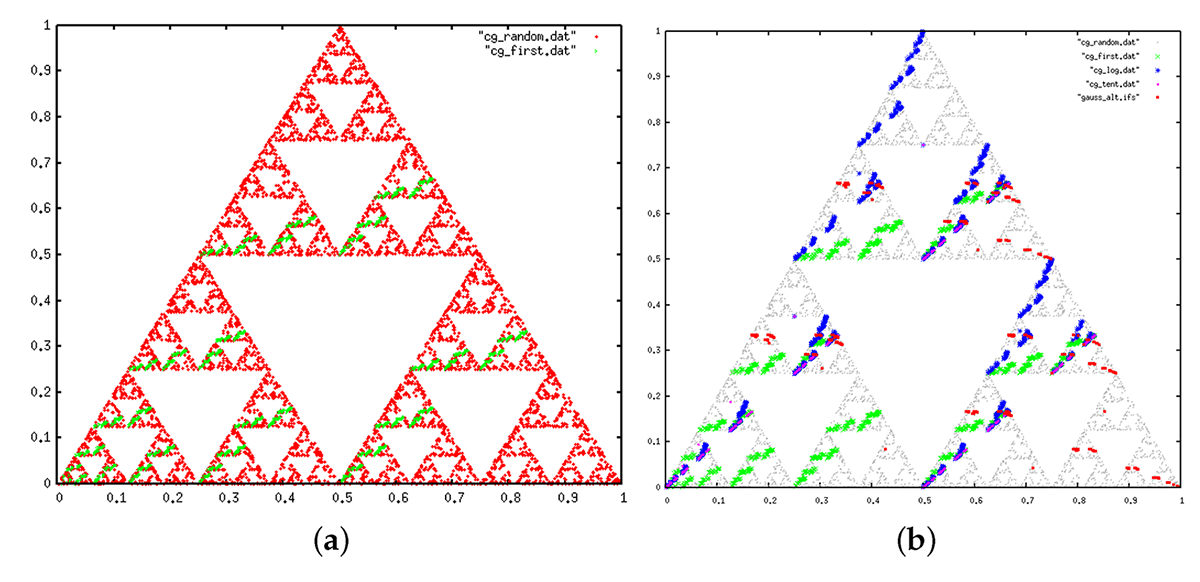
A las secuencias también se les aplica otro método llamado juego del caos, que consiste en generar una representación gráfica de las secuencias de símbolos con el método del sistema de funciones iteradas. Cuando se hace el juego del caos de un proceso aleatorio el patrón que genera el juego del caos es llamado atractor, por ejemplo en uno de los modelos nulos el atractor es el fractal conocido como triángulo de Sierpinski. Por el contrario, si el proceso no es totalmente aleatorio sólo generará parcialmente la figura de un proceso aleatorio.

En la secuencia de transición los valores de entropía denotaron aleatoriedad y al ser comparados con un modelo nulo en el juego del caos, se encontró que los patrones fractales asociados de ambas secuencias coinciden, “lo que confirma que la secuencia de transición tiene propiedades fuertes de aleatoriedad y no se puede distinguir de un proceso aleatorio” mencionan los investigadores en el artículo.

Análogamente, en la secuencia de residuos al dividir entre k existe una coincidencia con un proceso caótico, lo que permite afirmar que se observó un fenómeno no aleatorio en la secuencia.

Para la tercera secuencia de residuos del número de separación entre primos, su espectro de entropías de Rényi apunta a un fenómeno caótico; además su juego del caos genera parcialmente el triángulo de Sierpinski descartando aleatoriedad.

Sin embargo no fue posible calcular con exactitud los valores de entropía y la explicación de esta particularidad queda abierta. “Se trata de un patrón nuevo, no reportado previamente y esto sirve para agregar conocimiento a los números primos desde una perspectiva de la física de sistemas complejos”, explica Miramontes.

LIGAS:

Revista Entropy : http://www.mdpi.com/1099-4300/20/2/131/htm

Descargar el pdf