
Cuando la biología y la computación se unen para estudiar enfermedades humanas
La biología de sistemas estudia cómo las partes individuales de un sistema vivo interactúan para producir un comportamiento colectivo.
Ángel Calderón Flores y Aleida Rueda
25 de Agosto de 2023
En las últimas décadas, la biología ha sido atravesada por una revolución
tecnológica. Gracias a las ciencias ómicas (como la genómica, proteómica o
metabolómica, entre otras), es decir, aquellas que permiten estudiar un enorme
número de genes, proteínas y metabolitos, ahora es posible entender mejor cómo
se producen algunas enfermedades, como el cáncer o la diabetes tipo 2.
En esta revolución, la combinación de la biología y la computación ha sido clave,
pues ha abierto un nuevo campo de investigación: la biología de sistemas, que
busca entender los sistemas complejos vivos a través de la integración de múltiples
niveles de información. En lugar de estudiar las partes biológicas individuales de un
sistema, la biología de sistemas se enfoca en cómo estas partes interactúan para
producir un comportamiento colectivo.
Y lo hace a través del uso de modelos computacionales y tecnologías de alto
rendimiento. “La biología de sistemas busca condensar toda esta información (esas
grandes cantidades de genes o proteínas) en un conjunto para analizarlo a través
de herramientas como los modelos computacionales que integran esos datos y
ayudan a explicar cuáles son los mecanismos subyacentes en los sistemas vivos”,
explica Osbaldo Resendis Antonio, investigador de la Red de Apoyo a la
Investigación (RAI), el Instituto Nacional de Medicina Genómica (INMEGEN) y del
Centro de Ciencias de la Complejidad (C3).
Desde hace unos meses, Resendis, junto con el investigador Aaron Vázquez
Jiménez, también INMEGEN, ofrece un curso sobre Biología de Sistemas en el C3,
en el que exploran esta disciplina a un nivel introductorio, desde la regulación de
circuitos genéticos hasta redes en sistemas complejos.
“En el curso vemos desde la representación de redes de datos biológicos hasta
nuevas aplicaciones de frontera como la tecnología de RNAseq espacial y de célula
única, las cuales permiten caracterizar en dos dimensiones los perfiles de expresión
genética de células que componen la muestra de estudio”, explica el investigador.
Resendis y su equipo de investigación en el INMEGEN usan esta herramienta para
estudiar distintas enfermedades como el cáncer de mama. “Mediante el crecimiento
in vitro de líneas celulares de cáncer, actualmente es posible explorar el desarrollo
temporal de sus esferoides y, mediante estas tecnologías, determinar el perfil de
expresión de miles de células que lo conforman".
Esto es importante porque con ello pueden ver patrones de distribución y expresión
de los genes y, básicamente, determinar si una persona está sana o enferma.

Osbaldo Resendis y Aarón Vázquez
imparten curso introductorio de
Biología de Sistemas en el C3.
C3 UNAM
Modelos matemáticos y computacionales
Una de las herramientas más utilizadas para estudiar sistemas biológicos son los
modelos matemáticos, que son representaciones de la realidad que se quiere
analizar que se hacen a partir del lenguaje matemático.
Los modelos “tienen restricciones que nos permiten aislar variables y sólo
considerar las que deseamos”, dice Vázquez Jiménez, quien desarrolla modelos
matemáticos para medir la composición genética de organismos y entender el efecto
que tienen las reacciones químicas en las células.
“En biología, los modelos matemáticos son muy útiles porque permiten describir,
predecir y representar los mecanismos que experimentalmente no se saben,
determinar relaciones y explorar de una forma basta diferentes condiciones en
simulaciones virtuales”, explica el investigador del INMEGEN.
Un ejemplo es analizar la forma en la que un tratamiento afecta a las células. “Si queremos evaluar el efecto que tiene un fármaco en el crecimiento celular, en lugar de hacer el experimento en una zona de prueba, tenemos una representación matemática del efecto del fármaco sobre el crecimiento y podemos variar ese parámetro, relación o ecuación que represente esa interacción. De esa forma, el modelo ayuda a determinar y proponer las variables más relevantes que pueden ser probadas en el laboratorio”, agrega Vázquez.
Tanto Resendis como Vázquez han trabajado, justamente, en desarrollar modelos
matemáticos y computacionales que permiten diseñar y predecir el comportamiento
de sistemas biológicos. Por ejemplo, en un
artículo publicado en diciembre de 2022
en la revista Frontiers, los investigadores muestran que se pueden usar modelos
booleanos para estudiar y predecir la respuesta inmunológica en distintos tipos de
enfermedades como lo es el cáncer, ya que permiten simular cómo se comporta el
sistema en distintas condiciones y pueden ayudar a mejorar la eficacia de los
tratamientos actuales y desarrollar nuevos enfoques terapéuticos.
En otro artículo que publicaron en octubre de 2019 en la revista Scientific Reports,
los investigadores plantean que los modelos de vías de señalización justamente
señalan los procesos que ocurren dentro de las células y permiten la comunicación
entre ellas. Estas vías son esenciales para el correcto funcionamiento del organismo
y están involucradas en la reparación de tejidos. Además, examinan el papel de la
proteína LRRK2 en la vía de señalización Wnt/β-catenina y cómo su disfunción
puede contribuir a la enfermedad de Parkinson. Los resultados indican que la
LRRK2 interactúa con componentes clave de la vía de señalización, lo que sugiere
que podría ser un objetivo terapéutico potencial para la enfermedad de Parkinson.
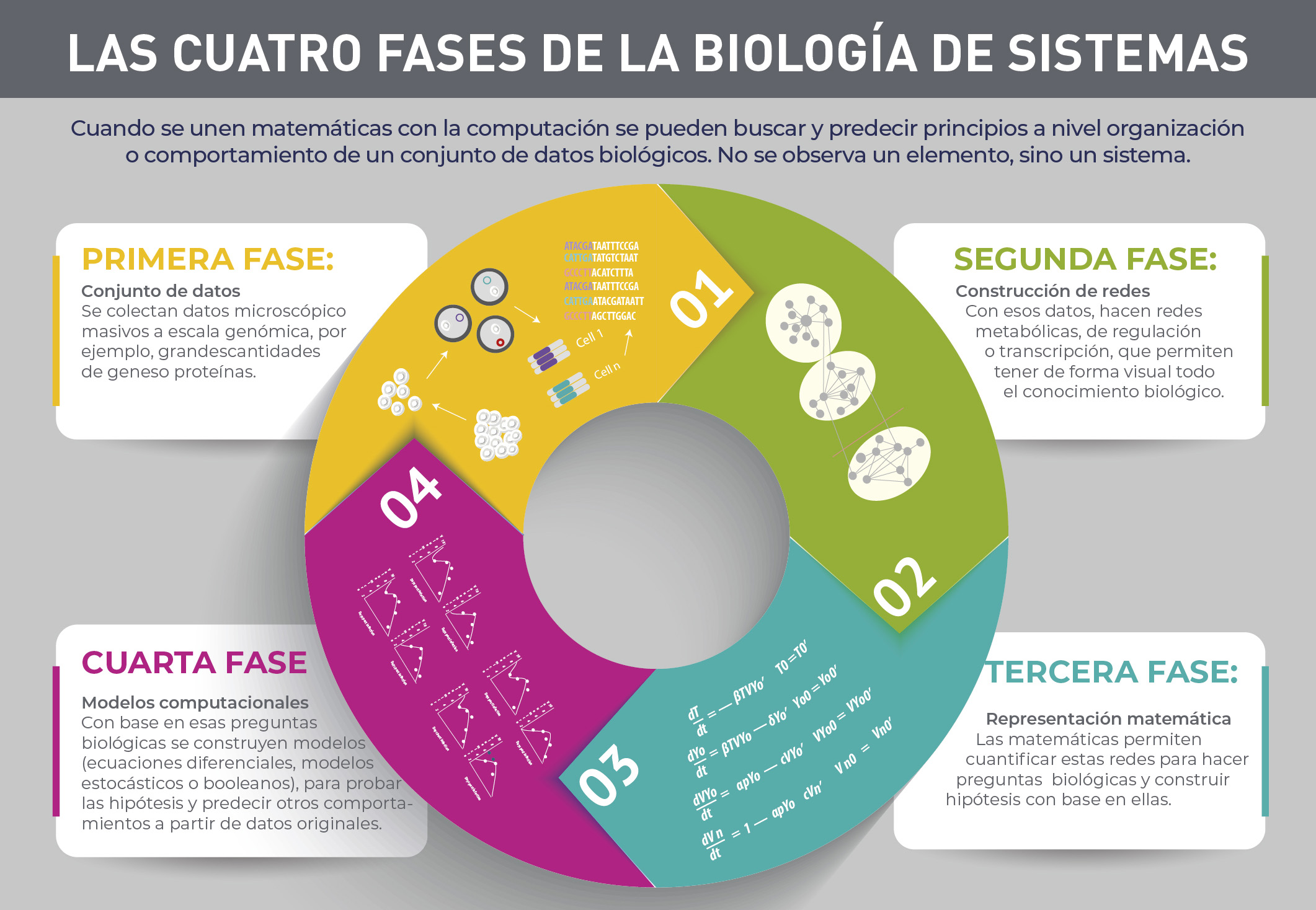
Pero no todos los modelos matemáticos usados en biología funcionan igual, ni
tienen los mismos objetivos. Existen diversos modelos que pueden usarse para
distintas metas (infografía).
La biología de sistemas encuentra aplicación en numerosas áreas de la medicina,
precisamente porque los modelos matemáticos son estupendas herramientas que
complementan la investigación y que pueden servir para entender mejor las
moléculas y su funcionamiento en distintos fenómenos biológicos.
“Si logramos modelos cuyas predicciones coincidan con las mediciones
experimentales con los miles de metabolitos, proteínas y genes, entonces tenemos
modelos entrenados para predecir e incluso para sugerir terapias. Por eso la
biología de sistemas es una base de la medicina personalizada. Ese es el objetivo:
tener un formalismo computacional que aplicado a una persona pueda sugerir cuál
sería la mejor estrategia de tratamiento”, explica Resendis.
Tanto Resendis como Vázquez consideran que un curso introductorio en biología de
sistemas puede ser de gran utilidad para prácticamente cualquier estudiante. “Este
campo requiere de estudiantes de distintas disciplinas. Normalmente estos grupos
están formados por personas de la física, matemática, biología, computación,
oncología, medicina, entre muchas otras disciplinas. En biología de sistemas es
fundamental conformar grupos de trabajo y hacer colaboraciones entre varias
disciplinas, definir un lenguaje en común, hacer preguntas de manera consensuada
… es definitivamente un campo interdisciplinario”.
Pero no todos los modelos matemáticos usados en biología funcionan igual, ni
tienen los mismos objetivos. Existen diversos modelos que pueden usarse para
distintas metas (infografía).
La biología de sistemas encuentra aplicación en numerosas áreas de la medicina,
precisamente porque los modelos matemáticos son estupendas herramientas que
complementan la investigación y que pueden servir para entender mejor las
moléculas y su funcionamiento en distintos fenómenos biológicos.
“Si logramos modelos cuyas predicciones coincidan con las mediciones
experimentales con los miles de metabolitos, proteínas y genes, entonces tenemos
modelos entrenados para predecir e incluso para sugerir terapias. Por eso la
biología de sistemas es una base de la medicina personalizada. Ese es el objetivo:
tener un formalismo computacional que aplicado a una persona pueda sugerir cuál
sería la mejor estrategia de tratamiento”, explica Resendis.

Tanto Resendis como Vázquez consideran que un curso introductorio en biología de sistemas puede ser de gran utilidad para prácticamente cualquier estudiante. “Este campo requiere de estudiantes de distintas disciplinas. Normalmente estos grupos están formados por personas de la física, matemática, biología, computación, oncología, medicina, entre muchas otras disciplinas. En biología de sistemas es fundamental conformar grupos de trabajo y hacer colaboraciones entre varias disciplinas, definir un lenguaje en común, hacer preguntas de manera consensuada … es definitivamente un campo interdisciplinario”.
Ligas de interés:
-
Página de Osbaldo Resendis:
https://resendislab.github.io/
-
¿Qué es la Biología de Sistemas?
https://www.um.es/acc/la-biologia-de-sistemas/
-
Seminario de Biología de Sistemas en el C3 de la UNAM
https://www.c3.unam.mx/seminarios/semi-biologiasistemas-2022.html
-
Artículo original en Frontiers :
https://www.frontiersin.org/articles/10.3389/fimmu.2022.1012730/full
-
Artículo original en Scientific Reports:
https://www.nature.com/articles/s41598-020-69026-7